Taban Aritmetiği Konu Anlatımı ve Çözümlü Sorular(RESİMLİ)

Taban aritmetiği konusu ÖSYM'nin KPSS, YGS, LYS ve diğer bütün sınavlarda çok fazla soru sorduğu konuların başında gelir. Ayrıca Matematiğin ilerleyen konularını daha kolay anlamanız için muhakkak bu konuyu çok iyi bilmelisiniz. 

TABAN ARİTMETİĞİ NEDİR? 

• Matematik işleminde kullanılan rakamların hangi rakamlardan oluşacağını ifade eder.  
• Günümüzde kullandığımız bütün sayı sistemi 10'luk sayı sistemine tabidir. Yani şuan kullandığımız taban aritmetiği 10'dur. 
• 10'luk sayı sisteminde sayılar : 0, 1, 2 , 3, 4 , 5 , 6 , 7 , 8  ve 9 rakamlarından oluşmaktadır. Yani 0 rakamı dahil toplam 10 rakamdan.
• Eğer taban aritmetiğimiz 5'lik sistemde olmuş olsaydı bu durumda rakamlarda kullanılacak rakamlar : 0, 1 , 2 , 3 , 4 rakamlarından oluşacaktı. Yani 0 rakamı dahil 5 rakamdan. 

10'LUK TABAN ARİTMETİĞİ 

456 rakamı üzerinden konuşalım. 

 

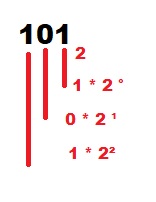
• 10'luk sistemde yukarıda ki örnekteki olduğu gibi rakamların altında 10 rakamının olduğu farz edilir. 
• Birinci basamaktaki rakam 100  (bir) rakamı ile çarpılır. 
• İkinci basamaktaki rakam 101 rakamı ile (10) ile çarpılarak sonuç bulunur. 
• Üçüncü basamaktaki rakam 102 rakamı ile (100) çarpılarak sonuç bulunur. 
• Daha sonra bütün basamaklardan çıkan sonuç toplanır. 

Örneğin : 3. basamaktaki 4 rakamı sadece bizler için 4 rakamını ifade etmektedir. Ancak 3. basamaktaki bu rakamın gerçek değeri için yukarıdaki işlemi yaptığımızda ( 4 x 102= 400) 400 değerinde olduğunu görüyoruz.  10'luk sistem de bu mantık gereksiz gözükebilir. Ancak diğer taban aritmetiği işlemlerinde bu mantığı öğrenmeniz çok önemlidir.  

2'LİK TABAN ARİTMETİĞİ BASAMAK DEĞERLERİ

 

FARKLI TABALARDA YAZILAN SAYILARI 10'LUK TABANA ÇEVİRME İŞLEMİ

• Bu konudan sınavlarda karşınıza en çok başka tabandaki bir rakamın 10'luk tabana çevrilmesi şeklinde sorular gelebilir. 
• Aşağıdaki çözümlü örnek sorular üzerinden konuyu iyice analiz etmeniz gereklidir. 

Çözümlü Soru 1 : 4 taban aritmetiğine göre olan (213)4 rakamının 10 tabanındaki değeri nedir?

Çözümü : 

 (213)4

Çözümlü Soru 2:  4 tabanında yazılan (3203)4 sayısının 10 tabandaki karşılığı kaçtır? 

Öncelikle bütün rakamları 4 kombinasyonunda tek tek hesaplamamız gerekli. 

• 3 x  4°  = 3 x  1 = 3 
• 0 x  4¹  = 0 x 4 = 0 eder
• 2 x  4²  = 2 x 16 = 32
• 3 x  4³  = 3 x 64 = 192

Sonuç : 192+ 32 + 0 + 3 =  (227)10 eder

10 TABANINDA YAZILAN SAYILARI 2, 3, 4, 5 , 6 , 7, 8 VE 9 TABANINA NASIL ÇEVİRİRİM?

Bu konudan sınavlarda sorulacak ikinci soru şekli 10 tabanında yazılan bir rakamın diğer taban değerini çevrilmesi sorusudur. 

• 10 tabanında verilen bir sayıyı hangi tabana çevirmemiz isteniyorsa eğer, sürekli o rakama böleceğiz. 
• Son bölüm değeri çevirmek istediğimiz taban değerinden küçük olana kadar sürekli böleceğiz. 
• Yaptığımız bütün bölme işlemlerinin ardından çıkan rakamın yanına tersten yazmak üzere kalan sayıları sırasıyla yazdığımızda işlemi tamamlamış olacağız. 

ÖRNEK : 27 sayısının 2'lik ve 4'lük  tabandaki değeri kaçtır? 

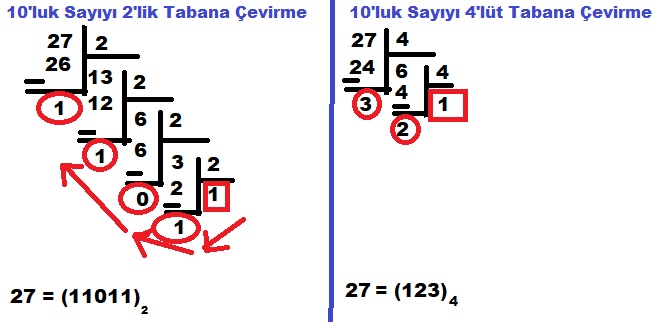
2'lik tabana çevirme işlemi açıklaması: 

• 27÷ 2 = 13 ve kalan 1'dir. 
• 13 ÷ 2 = 6 ve kalan 1'dir. 
• 6 ÷ 2 = 3 ve kalan 0'dır. 
• 3 ÷ 2 = 1 ve kalan 1'dir. 

Sonuç = 2710 = 110112  Daha kolay anlamanız için aşağıdaki resmi inceleyiniz. 

4'lük tabana çevirme işlemi açıklaması: 

27 4 = 6 ve kalan 3

6 4 = 1 ve kalan 2 

Sonuç : 27₁₀ = 123₄